Geometry

Written by Jane Jones (University of Winchester) and Clare Tope (Open University)

1.0 Overview

There is a variety of terminology used in different countries’ mathematics curricula to describe reasoning about the names and locations of shapes. In the England the term geometry is now used and we will use this term throughout. Geometrical language and understanding is needed by children to describe and understand location and movement, shape and size in the world around them. Geometry, although seemingly quite different to number, is still about looking for patterns and making connections but in this case it is within shape as opposed to number. Broadly speaking geometry is a part of mathematics in which visual thought is dominant (Barmby et al, 2009). Geometry involves playing with, manipulating, comparing, naming and classifying shapes and structures. Reasoning about the sizes and properties of shapes and their surrounding spaces helps children to make sense of the physical world and the word of mathematical shapes. Ryan and Williams (2007) argue that geometry offers children their first experiences of developing mathematical argument from the most informal justifications to the most formal proof. For example, the interior angles of any quadrilateral total 360°.

Van Hiele (1999) theory puts forward a hierarchy of levels of thinking about geometry. This theory has influenced thinking about geometry for several decades and is considered to be a well-established and important piece of research. You can read more about it in an article by Way (2011) on the Nrich website: https://nrich.maths.org/2487

This unit will focus on properties of shape and position and direction.

2.0 Key Ideas

2.1 Properties of shape

Pupils explore common 2-D and 3-D shapes, naming these and relating this to their knowledge of everyday objects. They should have the opportunity to recognise shapes in different orientations and sizes to allow them the opportunity to generalise about the common attributes a shape may possess. Children live in a 3-dimensional world of solid shapes but in order to fully describe, identify and classify these shapes we have to focus on the properties of the 2-dimensional surfaces.

2-D shapes can be sorted in different ways such as: the number of sides, the size of angles, the number of lines of symmetry or order of rotational symmetry. The learner will recognise an attribute common to a group of shapes (such as having 4 straight sides) and give the set a name (quadrilaterals). Further classification can lead to the creation of subsets within the group. For example, a subset of quadrilaterals is the group with 4 equal sides and 4 right angles which we call squares.

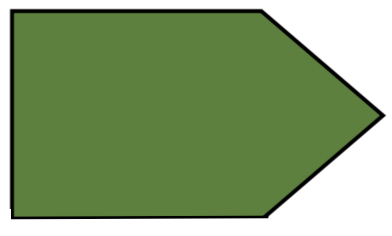
A 2-dimensional closed shape made up entirely of straight edges is called a polygon. Polygons can then be further classified depending on the number of sides. A regular polygon is one in which all the sides are the same length and all the internal angles are the same size. It is important for children to explore a range of non- prototypical examples of polygons to avoid children developing a limited understanding of ideas which may lead to misconceptions. See table below for the names and examples of different kinds of polygons:

Name	Number of sides	Regular	Irregular example
Triangle	3
Quadrilateral	4
Pentagon	5
Hexagon	6
Heptagon	7
Octagon	8

A similar classification of 3-D shapes is to separate those that have curved surfaces such a sphere, hemi-sphere, cylinder and cone. A 3-dimensional shape that is made up entirely of flat surfaces is called a polyhedron. To describe a 3-D shape we refer to faces, edges and vertices. 

• Face- A flat surface on a 3D shape
• Edge- A line where two faces meet
• Vertex- A point where two or more lines (edges or sides) meet

Name	Image	Number of faces	Number of edges	Number of Vertices
Cube		6	12	8
Cuboid		6	12	8
Square based pyramid		5	8	5
Triangular prism		5	9	6
Cylinder		3	2	0
Cone		2	1	0

2.2 Position and direction

Pupils use mathematical vocabulary to describe position, direction and movement of 2-d and 3-d shapes. There are three ways in which the position and direction of shapes can be ‘transformed’.

Transformations 

Reflection is a ‘flip’ over a mirror line. The shape is the same perpendicular distance in front and behind the mirror line and image is reversed. The shape still has the same size, area, and angles but it is a ‘mirror image’ of the original.

Rotation means turning a shape around a centre in either a clockwise or anti clockwise direction. The shaped is rotated through an angle and the turn is measured in degrees. The shape still has the same size, area, and angles but the orientation or direction has changed.

Translation simply means sliding a shape without rotating, resizing or changing orientation. Every point in the shape must move the same distance in the same direction.

The size of shapes can also be changed. This is the fourth translation and is called enlargement. The shape may become either bigger or smaller by a scale factor. 

Materials to support understanding of these terms can be found here:https://www.mathsisfun.com/definitions/transformation.html

Position 

Positioninvolves describing where something is located (it is often in relation to something else). We can describe: 

• positions on a 2-D grid using coordinates 

• movements between positions as translations of a given unit to the left/right and up/down. We can also use the coordinate system to describe these movements. 

Materials to support understanding of these terms can be found here:

https://www.mathsisfun.com/definitions/position.html

3.0 References

Barmby, P., Bilsborough, L., Harries, T. and Higgins, S. (2009) Primary Mathematics: Teaching for Understanding. Maidenhead: Open University Press.

Ryan and Williams (2007)Children’s Mathematics 4-15. Maidenhead: Open University Press. 

Van Hiele, P. (1999) Developing Geometric Thinking Through Activities that Begin with Play. Teaching Children Mathematics.February 1999, 310-316.

Way, J. (2011) The Development of Spatial and Geometric Thinking: the Importance of Instruction.