Numeracy for all (VSO)
|
|
Numbers and operations
Written by Jane Jones (University of Winchester) and Clare Tope (Open University) 1.0 OverviewAs part of their everyday life children need to be able identify numbers, estimate amounts and quantities and solve problems by choosing appropriate numbers operations and using them accurately. For this reason, number and operations are a central part of mathematical curriculum in the primary phase. Number includes a wide range of interconnected ideas which children come to understand through experiences which they represent using: pictures, symbols and language (Haylock and Cockburn, 2017). Over time children extend their ideas to include different kinds of numbers for example, they may begin with natural numbers such as 1, 2, 3 and extend their understanding to involve rational numbers such as ½, ¼. Enabling children to observe patterns and relationships and make connections is important as it allows children to develop insight and a ‘feel’ for numbers (Angileri, 2006). Developing an understanding of number concepts is also fundamental to becoming fluent in numerical calculation. Russell (2000) argues that children who are fluent in numerical calculation demonstrate flexibility in the computational methods they choose, understand and can explain these methods, and produce accurate answers efficiently. For more information about fluency and the importance of developing positive attitudes towards mathematics please see: https://www.youcubed.org/wp-content/uploads/2017/09/Fluency-Without-Fear-1.28.15.pdf 2.0 Key Ideas2.1 Counting and place valueCounting usually starts with reciting the number names in order for example, when a child counts out loud as they count steps or do their buttons up on their cardigan. This then progresses to the notion of numbers being ordered, the property of ordinality, with ‘four’ always coming after ‘three’. This is labelled the stable order principle which is one of 5 key principles associated with early counting. These were developed by Gelman and Gallistel (1978) and are listed below:
These are explored in more detail in the attached article by Thompson: https://www.ncetm.org.uk/public/files/712850/The+principal+counting+principles.pdf Later, children will be able to connect these experiences and language with a pictorial representation and finally a symbol. By watching, listening and copying, children will initially learn isolated facts but they can be encouraged to see the connections which underlie their use, for example, understanding the number 6 as a set of objects, as 3 sets of 2 objects, as a set of 1 object and 5 objects, as dots on a dice face, as a box of eggs.
Underpinning the re-arrangement of numbers is the concept of conservation of number, i.e. the understanding that a set of objects can be rearranged but the magnitude remains unchanged.
To represent numbers larger than 9 we use a place value system in which the digits 0-9 are placed in columns and zero is used as a place holder (denoting an empty ‘place’ within numbers and thereby ‘holding’ the position of the other digits). While our place value system is very powerful, Ross (2002) identifies that it requires an understanding of 4 fundamental ideas. These are:
Place value is an important concept and should be given plenty of time before moving pupils on to calculating with numbers. 2.2 Addition and subtractionThe operations of addition and subtraction emerge from counting. Two main structures for addition are:
The term aggregation refers to a situation in which (2 or more) quantities are combined and the operation of addition is used to determine the total. For example, there are 3 cakes on one plate and 5 on another, how many cakes are there altogether? This involves counting all the objects in the 2 sets. The term augmentation refers to a situation where a quantity is increased by an amount and the operation of addition is required to find the increased amount. For example, Jane has 3 cakes and is given 7 more, how many cakes does she have now? This involves counting on from 3. Children should be encouraged to realise that 3 + 7 = 7 + 3 and it is more efficient to count on from a larger number. There are also two main structures for subtraction, these are:
The reduction structure refers to a situation in which a quantity is removed in some way or other and subtraction is required to calculate how many or how much remains. For example, there are 16 sweets in the tin and 5 are eaten, how many are left? The comparison structure refers to those situations where subtraction is required to make a comparison between two quantities. Subtraction allows us to determine the difference between the two amounts. For example, Billy is 12 and Sophie is 7. How much older is Billy than Sophie? The context suggests counting up from 7 to 12 to find the difference. Materials to support understanding of these ideas can be found on the NCETM website:
As understanding of addition and subtraction grows, children should make connections between the 2 operations. For example, having worked out that 7 + 3 makes 10, they can then explore what happens when the 3 is subtracted. They will realise that the answer is 7, this is described as an inverse relationship between addition and subtraction. 2.3 Multiplication and divisionMultiplication and division also emerge from counting, for example counting in groups of 3. This is the starting point for developing the conceptual understanding which underpins multiplication and division facts. There are two main structures for multiplication, these are:
The repeated aggregation structure refers to the idea that multiplication can be seen as repeatedly adding same sized groups. For example, 7 + 7 + 7 is recorded as 7 x 3. The scaling structure is a rather more difficult idea and can be seen as an extension of the augmentation structure of addition. With scaling we also see a change in a quantity, we increase it by a scale factor. For example, Ann has 3 times more sweets than her brother Robert. If Robert has 5 sweets, how many sweets does Ann have? There are two main structures for division, these are:
The equal sharing structure refers to the idea of sharing a quantity equally between a given number of portions and we are asked to determine how many there are in each portion. For example, 20 sweets might be shared equally between 4 children at a party, the calculations which corresponds to this situation is 20 ÷ 4. The grouping structure interprets 20 ÷ 4 in a different way. Now the question being asked is how many groups of 4 are there in 20. So the process of sharing out 20 in the example above can be thought of as repeatedly subtracting sets of 4 from the set of 20 until there are none left, counting the number of sets as you do this. Materials to support understanding of these ideas can be found on the NCETM website:
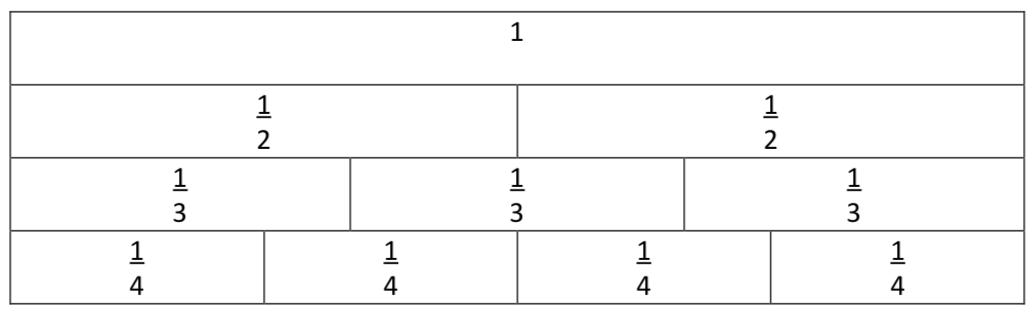
Children should also experiment with ideas and develop an understanding that multiplication is commutative and that multiplication and division are inverse operations. 2.4 FractionsChildren first encounter fractions in a range of real life situations such as sharing an apple or a bag of marbles. The concept of a fraction is beginning to emerge but it is not yet refined. From this starting point they gradually establish that the parts must be equal and that halves are what you get when you share a whole thing into 2 equal parts and that quarters are 4 equal parts. Children will encounter situations where they find fractions of a whole and where they find fractions of a set: For example, 1 whole divided equally into 2, 3, or 4 parts which is recorded pictorially or using fractions notation. See diagram below.
To find a quarter of 12, a set of 12 counters is divided equally into 4 equal groups. So a quarter of 12 is 3.
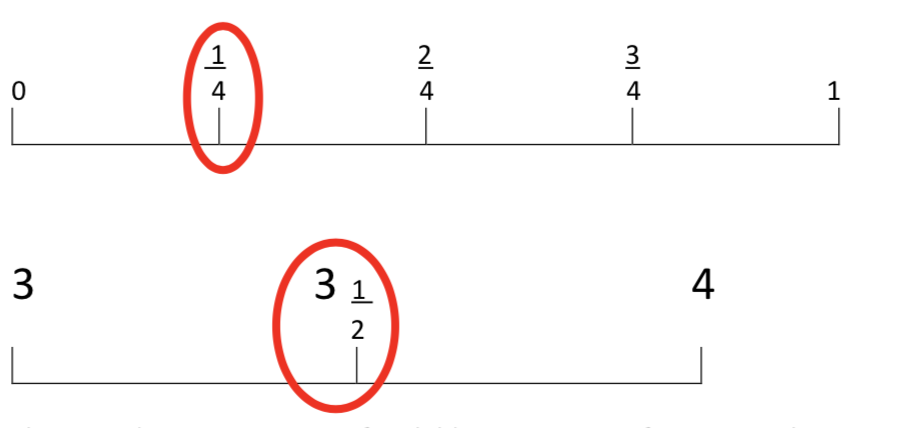
A further aspect of the understanding of fractions that children will develop in primary school is that fractions can represent a point on a number line. Children can now see a new set of numbers that lie between the natural numbers they are familiar with. For example, 1⁄4 lies between 0 and 1, 3 1⁄2 is between 3 and 4.
This provides an opportunity for children to count in fractions in the same way as they will have previously counted in whole numbers. An example of this can be seen here: https://vimeo.com/83486101 You and the children should use the language of 'numerator' and 'denominator' to describe the top and bottom numbers in a fraction, to allow for clear communication. An article which identifies some of the complexities associated with the teaching of fractions can be found here: https://highlandnumeracyblog.files.wordpress.com/2015/01/nunes-et-al- fractions_difficult-but-crucial-in-mathematics-learning.pdf 3.0 ReferencesAnghileri, J. (2006)Teaching number sense. 2ndedn. London: Continuum. Boaler, J. (2015)Fluency Without Fear: Research Evidence on the Best Ways to Learn Math Facts. Published by Youcubed. Available at:https://www.youcubed.org/wp-content/uploads/2017/09/Fluency-Without-Fear-1.28.15.pdf Gelman, R. & Gallistel, C. (1978) The Child's Understanding of Number. Cambridge: MA. Harvard University Press. Haylock, D. and Cockburn, A. (2017) Understanding Mathematics for Young Children: A guide for teachers of children 3-7. 5thedn. London: SAGE Publications Ltd. Nunes, T, Bryant, P, Hurry, J and Pretzlik, U. (2006) Fractions: Difficult but crucial in mathematics learning. Teaching and Learning Research Briefing, 13. Available at:https://highlandnumeracyblog.files.wordpress.com/2015/01/nunes-et-al-fractions_difficult-but-crucial-in-mathematics-learning.pdf Ross (2002) ‘Place value: Problem solving and written assessment’, Teaching Children Mathematics, 8(7), 419-23. Russell, S. (2000) Developing Computational Fluency with Whole Numbers.Teaching Children Mathematics, 7, (3), 154-158. Thompson, I. (ND) The principle counting principles. Published by NCETM. Available at:https://www.ncetm.org.uk/public/files/712850/The+principal+counting+principles.pdf |