Key Teaching/Pedagogical issues
This column highlights the major pedagogical considerations when teaching mathematics. The research mentions a major factor stopping children achieving in mathematics is a fixed mindset” i.e. a child’s belief, and that of their parents and teachers that they cannot achieve in this subject. In fact neurological research suggests that the capacity of the brain to learn is not limited by age.
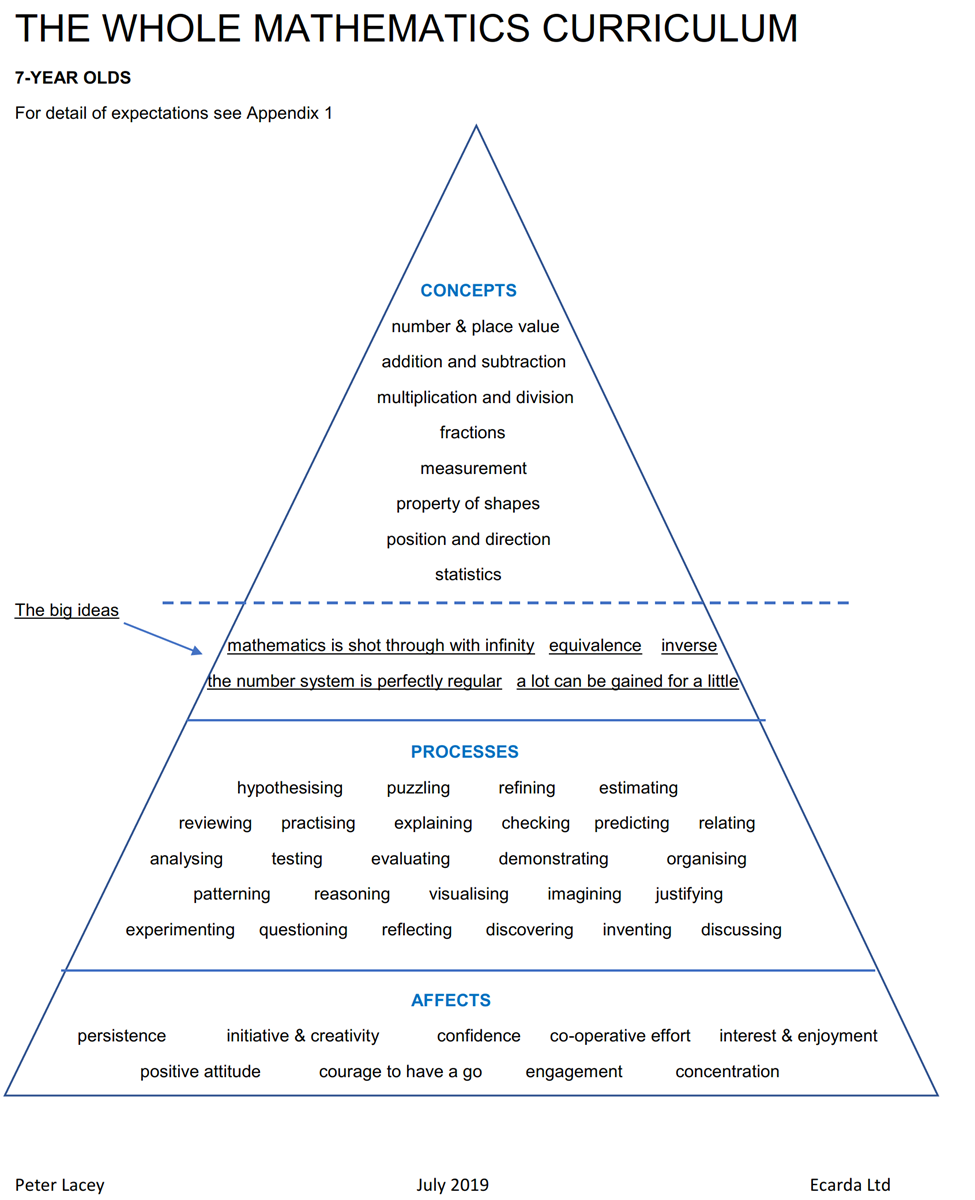
The triangle (by Peter Lacey) below outlines the key concepts covered in many countries' primary curricula and in this MESHGuide, and the following article by Dr. Jenefer Golding provides considerable detail about how to teach mathematics effectively. See Teaching Approaches Overview for more of Peter Lacey's work.
Appendix 1 The Information in columns two and three provide in-depth explanations of the concepts in the triangle.
Pedagogies for teaching numeracy to all
Dr Jenefer Golding, University College London, Institute of Education. (see also in this MESHGuide: Approaches to teaching Numeracy for all and developing mathematical thinking and Summary for volunteers, parents, brothers and sisters)
Approaches to teaching numeracy are outlined elsewhere, and the evidence for those given. Here we give more details of the tools and specific ideas that can or should be used to give children early confidence and fluency with mathematical ideas. We indicate the progression they will make in their learning, in whatever setting that takes place. Many children move from home/local community, maybe through pre-school provision, to primary school. Those moves happen at different ages, and children in any case develop at different paces, but they all need the same range of experiences to build on and support their later mathematical development. Informal experiences, especially talking about number/pattern/space/shape/time/measure, but also the use of play opportunities, including role play, stories, rhymes, songs, games and dances, are helpful from a very young age, and well into primary education. The NRICH Early Years activities provide good examples of this approach, with problem solving providing opportunities for creative and critical thinking through stories and rhymes, as well as classroom routines such as tidying up or sharing fruit. This approach helps develop ‘children’s readiness for school/formal learning’ by fostering confidence and curiosity, which should be the priority goal.
The most productive learning, in whatever setting, starts from such opportunities, with interaction with other children and resources (selected to stimulate particular mathematical thinking). It includes constructive interaction with an adult - to set up experiences, gently guide the learner, model mathematical language and sometimes give them new information, always communicated with meaning rather than as something to be learned by rote. It includes opportunities for problem solving and projects to engage and motivate learners to apply skills and learn new ones.
Below, we consider each area of numeracy in turn, and suggest suitable approaches to the ideas children should engage with as they move from pre-school through early primary, and the locally available or improvised resources that would especially support that. These suggestions are further expended in other documents that concentrate on just one area. Details of a good progression are given in the research-based New Zealand documents given below: those will work for any education system, but children’s prate of progress might vary, depending on the opportunities, experiences, and resources that have been available for them.
Numeracy area: Number sense
Effective pedagogy uses stories, songs, and play/everyday situations, including stones, bottle tops, feathers, … to talk with children about
• understanding more/less as important ideas, ‘knowing’ how many in a group of up to 5 objects without counting (subitising)
• counting with understanding (including finger counting and relative size of numbers), numeral recognition
- sorting by different characteristics
- applying counting to simple addition and subtraction problems, and making equal shares, first using numbers 1 to 10 and then gradually increasing the range of numbers they work with, including to using simple fractions, and to 0. Children are fascinated by the fact that numbers go on for ever: encourage that fascination.
The emphasis should always be first on ‘developing number sense’ and only then on ‘finding the answer’, though in the longer term, we want children to be able to do both of these.
- As children develop, teachers will use a 100-square they have made, like the one given, to show and talk about the patterns in how we say and write whole numbers, and children will ‘find one more than’, ‘one less than’, find ‘ten more than’ ….. and other games with the 100-square (evens/odds, multiples of 2 or 3 or 5 or 9…). They will begin to understand ‘place value’, e.g. that 57 is made of 5 10’s and 7 ones. That is important as a foundation for learning written calculations, whether those are set out horizontally or vertically.
- Teachers will make and use a numberline with chalk on the floor, string or on the wall, that children can use to relate whole numbers, fractions, and eventually, decimals and negative numbers. As in the picture, they can move to using a ‘blank’ numberline to understand calculations and support flexible thinking with numbers. Children will eventually begin to understand that there are ‘more’ numbers in between every pair of numbers they have marked on the numberline, and will place fractions in the right places between whole numbers…
- Children practise their number skills, and counting backwards/forwards in different ‘jumps’ perhaps using a counting stick the teacher has made, as at https://garyhall.org.uk/counting-stick.html. More ideas for using counting sticks can be found at https://www.broadbentmaths.com/pages/newspage_223611.cfm
- Children are encouraged to ‘play’ with numbers, perhaps making up stories or questions that involve a particular situation or calculation, and relating the number work they learn to everyday situations. Teachers use an increasing range of whole numbers, fractions and decimals and build up children’s understanding and skills with addition, subtraction, multiplication, and division (as either sharing or grouping), and will explain what they are doing to other children and to adults. Eventually, children will have fluent (quick, reliable and flexible) recall of ‘number bonds’ to 20 (the sum of two numbers that add to 20) and can rapidly think beyond those; they will recall first easier times tables, such as 2,5,10. If they know those ‘number facts’ without effort, they have more ‘thinking space’ available for applying those facts in mathematical situations.
Numeracy area: Pattern and structure
- Pre-school children have opportunities for recognising, creating and describing repeating patterns with objects (e.g. beans), sounds, movements, and eventually with numbers. To do this, teachers help them use a variety of objects, and to group helpfully.
- They have informal opportunities to recognise, create and describe shape and size, regularity, and symmetry (e.g. building structures, making tiling pattern), working with everyday shapes and with drawings. Throughout, children are encouraged to talk about these ideas, important for a foundation for their thinking.
- As children move up primary schooling, teachers give them opportunity to recognise, create, continue and record patterns that use shape or number, and to puzzle out and predict what for example the 20th shape in a pattern will be, or the 100th number, giving reasons for that, or identify and explain patterns they see in a sequence of calculations. They let children puzzle over harder challenges, and encourage them to explain their solutions to one another.
- Structure of number and number operations: Children are helped to notice and understand that the ones/tens/hundreds structure of our whole number notation can be extended (and to small numbers, using decimals), and fractions/decimals inserted between whole numbers in regular ways. They begin to see subtraction as the ’reverse’ of addition, and division as the reverse of multiplication, and to use that. They recognise that the order of numbers does not matter for +/x, but it does for -/÷, and that many calculations can be achieved in a variety of ways, depending on the numbers involved.
Numeracy area: Spatial awareness and geometric thinking
- Teachers give children opportunity to talk about position and direction concepts and language in relation to their own body and other objects (e.g. inside/outside, under/over, left/right etc.). Children might learn to follow instructions about movement, perhaps through dance or games, and will be encouraged to act out stories that have these ideas in them.
- Children are supported to recognise, talk about and represent, in different ways, two- and three-dimensional shapes and objects (e.g. sorting, naming basic shapes, describing what is the same and what is different about two shapes, using gesture and body movement, tracing & drawing, building with materials….)
- As children move into lower primary classes, they will begin to distinguish between different sorts of triangles or quadrilaterals, or angles, and eventually come to be able to measure and use lengths and angles within 2-D and 3-D shapes
Numeracy area: Measurement thinking
- Supported talk pre-school will develop children’s awareness of measurement attributes and direct comparison (e.g. longer, heavier, larger, taller, higher, holds more etc.) They begin to see these measures as ‘conserved’ – fixed – properties of objects, not changing as objects are moved.
- Adults will encourage children to use informal units and apply counting (how many steps, cups, stones etc., is it taller than you, do you think this is longer or shorter than your hand?) They encourage children to estimate their responses, and then to check those by using accurate comparison and informal measurement.
- Adults talk about the passing of time and time sequences (events, routines, seasons, days) and draw children’s attention to their use of digital or analogue clocks, and uses of time (telling time on the hour).
- Children are supported to make sense of money and other exchange, and of budgeting, especially in naturally occurring situations, but also in role play and through stories, written or oral.
As children move through early primary, their teachers help them come to use more standard units of measure, such as metre rules, and might support their class in making their own metre rules: https://aiminghigh.aimssec.ac.za/years-3-7-metre-measures/ They help children come to know other familiar units. For example, if sugar is sold locally in 1 kg bags, they will repeatedly support children in linking a kg with the weight of a bag of sugar, or 200g with the weight of a mango… They will help children come to know how tall they are, and how tall the teacher is. They will talk about ‘one hour until it’s time to go home’, or ‘you can go outside for 20 minutes’. Such approaches give children a ‘picture’ of standard measurement units, so that they can use them with meaning-making. Teachers help children make links between their number work and local currency, in different depths since different currencies use numbers of different sizes.
Teaching talk, recording and assessment including questioning (connects with characteristics of effective learning: see ‘approaches to learning’)
- Eventually primary children will need to learn to communicate and record their mathematical thinking in ways that other people can understand. Initially this might include encouraging children to ‘draw pictures’ of what is happening in a maths story. Children’s awareness of symbolic representation of number and other mathematical concepts can eb developed from an early age, by pointing out where that occurs in the environment or any available books.
- The ‘teaching approaches’ section explains why teacher-children talk, and child-child talk, are both important in building up children’s learning, and their ability to communicate mathematically, and suggests classroom routines that can support development of talk.
- Such opportunities also give adults, or teachers, a chance to assess what children know and understand. Adults who know children well can ask them questions tat are well-pitched to move on their understanding to the next step.
- Good pedagogy does not stop at straightforward, closed questions, but might ask a group of children or whole class:
- What is the same and what is different about these two shapes/numbers/toys/stones?
- Is it sometimes, always or never true that…. We can share a pile of oranges fairly between a group of children/When you multiply two numbers the answer is always bigger/all squares are rectangles/when you add two odd numbers you get an even answer…. ?
- How many different ways can you fill the boxes? □□ + □ = □□□
- What happens if you fold a square piece of paper in two and then cut across a corner/you sit every child in the class in a circle and then ask each second/third/fourth child sitting down to stand up/you cross out all the multiples of 3 on a 100-square…?
- What else can do you know is true if 8 + 5 = 13 / 54 x 3 = 162 / 1 hour = 60 minutes / there are 10 mm in each cm?
- What do you notice? 5 + 12 = 17, 15 + 12 = 27, 25 + 12 = 37…..
- Which is the odd one out? 3, 7, 8 / 3 different triangles, two of which have something in common/ ½, 50%, 2/3
Notice that each of these question stems can be widely used at an appropriate level for the children present, makes children thinking much harder than a ‘closed’ question, can be given to children to talk about in pairs or 3’s, and their responses tell the adult quite a lot about their mathematical knowledge and thinking.
Key ideas are that children come to enjoy mathematics, to talk about it, and to have opportunity to engage actively with mathematical ideas so they come to have meaning.
The resources on the AIMSSEC website (below) are all based on reliable research and have been trialled in areas with large classes and low resources. They are mostly designed for use with slightly older children, but the approaches can easily be adapted for pre-school or lower primary children:
https://aiminghigh.aimssec.ac.za/manage-your-own-professional-development-workshops/ https://aiminghigh.aimssec.ac.za/advanced-search/ https://aiminghigh.aimssec.ac.za/category/lesson-activities/
The content of this chapter is drawn from the following research-based work:
Kuhne, C., O’Carroll, S., Comrie, B., & Hickman, R. (2013). Much more than counting: Supporting mathematics development between birth and five years. The Schools Development Unit (UCT) and Wordworks Cape Town http://www.wordworks.org.za/wp-content/uploads/2017/01/More-than-Counting_web.pdf
Gifford, S. (2014) A good foundation for number learning for five-year-olds? An evaluation of the English Early Learning ‘Numbers’ Goal in the light of research, Research in Mathematics Education, 16:3, 219-233
Institute for Educational Practice (2014) Teaching math to young children. Available at http://ies.ed.gov/ncee/wwc/PracticeGuide.aspx?sid=18.
New Zealand Ministry of Education. (2010a). Number: Early learning progression. Wellington. Retrieved from http://www.nzmaths.co.nz/number-early-learning-progression?parent_node=
New Zealand Ministry of Education. (2010b). New Zealand curriculum and standards. Wellington. Retrieved from http://www.nzmaths.co.nz/level-one-number-and-algebra
Sim, M., Bélanger, J., Hocking, L., Dimova, S., Iakovidou, E., Janta, B. & Teager, W. (2018) Teaching, pedagogy and practice in early years childcare: an evidence review Available at https://www.eif.org.uk/files/pdf/teaching-pedagogy-and-practice-in-early...
The Nrich project based at the university of Cambridge: https://nrich.maths.org/early-years